The digital world is binary(da_what3)
What is Binary?
Binary is a scheme of numbers that only has two possible values for each digit: 0 and 1. The term also describes any encoding/ decoding system in which there are only two possible states. In digital data storage, memory, communications, or processing the 0 and 1 values are sometimes called "low" and "high" or "On" and "Off".
The digital world is represented in binary, but hexadecimal, which is compatible with binary and more easily understood by people, is commonly used. Like previously mentioned, binary uses only the numbers 0 and 1. However, in some cases L/H is used as a counterpart to 0/1 notation.
In order to indicate which base is used, d(decimal), b(binary), and h (hexadecimal) are added to the end of the number.
Base 10=Decimal Base 2=Binary Base 16=Hexadecimal
Example
11d(11 in decimal)、11b(3 in decimal)、11h(=17d)
Decimal, Binary, and Hexadecimal Conversion
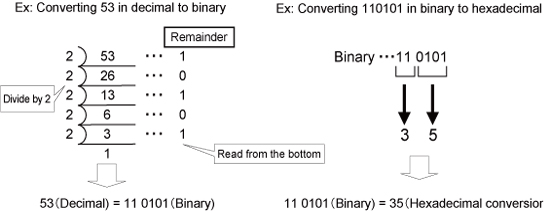
Decimal, Binary, And Hexadecimal Conversion Examples
| Decimal | Binary | Hexadecimal | ||
|---|---|---|---|---|
| 63 | 0000 0011 1111 | 0 | 3 | F |
| 127 | 0000 0111 1111 | 0 | 7 | F |
| 255 | 0000 1111 1111 | 0 | F | F |
| 1023 | 0011 1111 1111 | 3 | F | F |
| 4095 | 1111 1111 1111 | F | F | F |
Important Numbers to Remember
Increasing a binary number by one digit can double the value.
The values in red are often used by A/D and D/A converters.
3bit=8combinations 4bit=16combinations 5bit=32combinations 6bit=64combinations 7bit=128combinations 8bit=256combinations 9bit=512combinations 11bit=2048combinations12bit=4096combinations 14bit=16384combinations 16bit=65536combinations
What Are Bits?
A single binary digit, which is either 0 or 1, is also referred to as a bit.
electronics_tips_menu