What are A/D and D/A converters?(da_what1)
A/D Converter and D/A Converter
<What are A/D and D/A converters?>
D/A Converters
D/A converters convert digital signals into analog format.
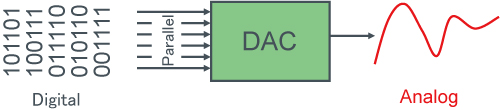
- Digital Data:
- Evenly spaced discontinuous values
- Temporally discrete, quantitatively discrete
- Analog Data (Natural Phenomena):
- Continuous range of values
- Temporally continuous, quantitatively continuous
A/D Converters
An A/D converter is a device that converts analog signals (usually voltage) obtained from environmental (physical) phenomena into digital format
Conversion involves a series of steps, including sampling, quantization, and coding.
A/D and D/A Requirements
Electrically sophisticated and high-speed processing are performed digitally in CPUs and DSPs.
Natural phenomena are converted to digital signals using an A/D converter for digital signal processing, then converted back to analog signals via a D/A converter.
Advancements in Microfabrication Technology→Signal Processing Digitization
→A/D and D/A Converters Required

A/D Converter Applications
- Digital Audio:
- Digital audio workstations, sound recording, pulse-code modulation
- Digital signal processing:
- TV tuner cards, microcontrollers, digital storage oscilloscopes
- Scientific instruments:
- Digital imaging systems, radar systems, temperature sensors
D/A Converter Applications
- Digital Audio:
- CD, MD, 1-bit Audio
- Digital Video:
- DVD, Digital Still Camera
- Communication Equipment:
- Smartphones, FAX, ADSl equipment
- PCs:
- Audio, video cards
- Measurement instruments:
- Programmable power supplies, etc.
Basic Operation of a D/A Converter
A D/A converter takes a precise number (most commonly a fixed-point binary number) and converts it into a physical quantity (example: voltage or pressure). D/A converters are often used to convert finite-precision time series data to a continually varying physical signal.
An ideal D/A converter takes abstract numbers from a sequence of impulses that are then processed by using a form of interpolation to fill in data between impulses. A conventional D/A converter puts the numbers into a piecewise constant function made up of a sequence of rectangular functions that is modeled with the zero-order hold.
A D/A converter reconstructs original signals so that its bandwidth meets certain requirements. With digital sampling comes quantization errors that create low-level noise which gets added to the reconstructed signal. The minimum analog signal amplitude that can bring about a change in the digital signal is called the Least Significant Bit (LSB), while the (rounding) error that occurs between the analog and digital signals is referred to as quantization error.
Basic Operation of an A/D Converter
Now, let's take a look at the basic operation of an A/D converter.
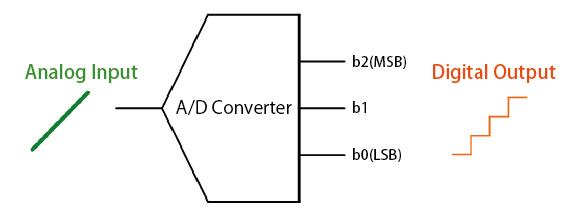
The A/D converter breaks up (samples) the amplitude of the analog signal at discrete intervals, which are then converted into digital values. The resolution of an analog to digital converter (indicating the number of discrete values it can produce over a range of analog values) is typically expressed by the number of bits. In the above case of a 3bit A/D converter, the upper value (b2) is referred to as the Most Significant Bit (MSB) and the lowest value (b0) the Least Significant Bit (LSB).
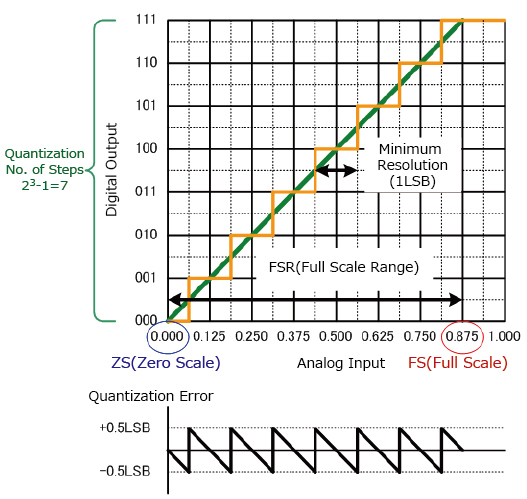
The graph below shows the relationship between the analog input and digital output.
In addition, the first digital change point (000→001) below 0.5LSB is the zero scale, while the last digital change point (110→111) is termed full scale and the interval from zero to full scale referred to as the full scale range.
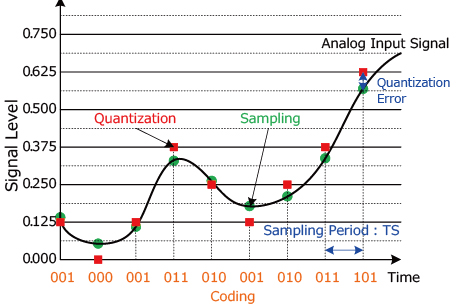
Analog Signal to Digital Signal Conversion Methods
- Sampling:
- Sampling is the process of taking amplitude values of the continuous analog signal at discrete time intervals (sampling period Ts).
[Sampling Period Ts = 1/Fs (Sampling Frequency)]
Sampling is performed using a Sample and Hold (S&H) circuit. - Quantization:
- Quantization involves assigning a numerical value to each sampled amplitude value from a range of possible values covering the entire amplitude range (based on the number of bits).
[Quantization error: Sampled Value - Quantized Value] - Coding:
- Once the amplitude values have been quantized they are encoded into binary using an Encoder.
A/D , D/A Converter
Data ConverterDownload datasheet
ROHM offers a broad portfolio of data converters, including A/D converters, D/A converters, and Audio CODECs.
electronics_tips_menu